Pierwotnie kryptografia była mistyczną formą sztuki, której celem było ukrywanie informacji przed nieautoryzowanymi osobami. Na przykład prosta metoda szyfrowania wiadomości została opracowana przez Gajusza Juliusza Cezara około 100 roku p.n.e. Podstawową ideą tej metody było przesunięcie każdej litery w alfabecie o ustaloną wartość, która służyła następnie jako tajny klucz. Na przykład, gdyby Cezar zaszyfrował Veni, vidi, vici tajnym kluczem 3, uzyskałby – używając 26 liter alfabetu angielskiego – zaszyfrowany tekst Yhql, ylgl, ylfl.
Jednak metoda została szybko rozpracowana, następnie ulepszona, ponownie złamana i tak dalej. W ten sposób na przestrzeni czasu można było zaobserwować swego rodzaju grę w kotka i myszkę między projektantami metod szyfrowania a atakującymi, którzy łamali te metody, by uzyskać dostęp do tajnych informacji. Trwało to aż do lat 80., kiedy to odkryto szyfrowanie, którego bezpieczeństwo można udowodnić.
Bezpieczeństwo, które można udowodnić (lub: oparte na dowodach), to dziedzina, która ma na celu ocenę bezpieczeństwa systemów za pomocą dowodów matematycznych. Ludzie często myślą o kryptografii jako o morzu cyfr i ogromnych liczb – i faktycznie, tak często jest. Jednak dla matematyka szczegóły takie jak konkretne wartości są nieistotne: najważniejsze jest symboliczne zdefiniowanie systemu w sposób, który nadaje się do przeprowadzenia logicznego dowodu. Rozwój dającego się udowodnić bezpieczeństwa wprowadził do starożytnej praktyki kryptografii, która kiedyś była uważana bardziej za sztukę niż naukę, niezbędny rygor właściwy naukom ścisłym.
W tym artykule przedstawimy podstawy bezpieczeństwa, które można udowodnić, oraz powiązane zasady pracy na przykładzie analizy komunikacji przez pocztę elektroniczną. Opiszemy również kilka typowych błędów w stosowaniu metod kryptograficznych, a także mocne strony i ograniczenia bezpieczeństwa opartego na dowodach. Na koniec użyjemy praktycznych przykładów, aby zilustrować aktualne tematy badawcze w dziedzinie współczesnej kryptografii.
Bezpieczeństwo oparte na dowodach: 6 kroków
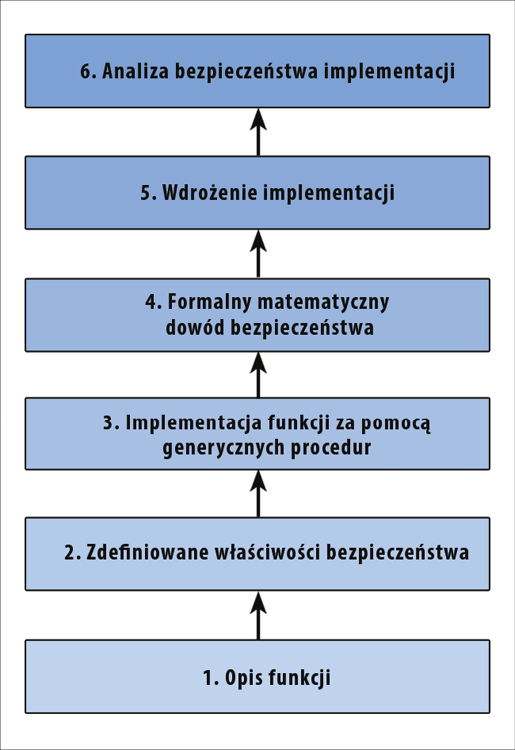
Zgodnie z zasadami projektowania z myślą o bezpieczeństwie (security-by-design) proces implementacji bezpieczeństwa opartego na dowodach składa się z sześciu etapów, jak pokazano na Rysunku 1.
Krok 1: Opisz funkcjonalność
Pierwszym krokiem jest opisanie funkcjonalności systemu: jaki jest jego cel? Opis ten często przybiera formę specyfikacji wymagań.
Krok 2: Zdefiniuj właściwości bezpieczeństwa
Zadanie definiowania cech bezpieczeństwa składa się zwykle z dwóch części. Najpierw musimy opisać cele bezpieczeństwa w sposób zrozumiały dla każdego. Następnie musimy dokładnie sformalizować całość, aby uniknąć niejednoznacznych interpretacji.
Należy zauważyć, że formalny aspekt bezpieczeństwa zależy od formalnego opisu. Dlatego ta formalizacja musi jak najdokładniej uwzględnić rzeczywiste cele ochrony. Z reguły ten krok obejmuje następujące aspekty: jakie aspekty bezpieczeństwa musi zapewniać system? O jakich systemach i z jaką konfiguracją mówimy? Przed jaką klasą atakujących musimy się obronić? Jakie są ich możliwości? Kiedy atak uznaje się za udany?
Identyfikacja i sformalizowanie aspektów bezpieczeństwa jest trudnym zadaniem, a odpowiedni model bezpieczeństwa nie został jeszcze znaleziony dla wielu schematów kryptograficznych. Na przykład społeczność naukowa wciąż nie uzgodniła definicji szyfrowania uwierzytelnionego [1]. Ponadto zawsze istnieje naturalna konkurencja między wydajnością a bezpieczeństwem. W idealnej sytuacji zapewnilibyśmy sobie ochronę przed wszystkimi typami atakujących i korzystali z najlepszych możliwych gwarancji bezpieczeństwa. W praktyce jednak bezpieczeństwo nie jest darmowe, a silniejsze gwarancje bezpieczeństwa często przekładają się na mniejszą wydajność – a niewielu lubi korzystać z mało wydajnych systemów.
Krok 3: Implementuj funkcje za pomocą ogólnych procedur
Ten krok odnosi się do podstawowych elementów kryptograficznych, takich jak szyfrowanie kluczem prywatnym, kody uwierzytelniania wiadomości, funkcje skrótu lub schematy podpisów. Zdefiniowanie ogólnych procedur pomaga zrozumieć, która właściwość zabezpieczeń podstawowego bloku konstrukcyjnego jest używana do uzyskania określonej właściwości zabezpieczeń nowego systemu.
Projekt musi działać niezależnie od konkretnych procedur, ponieważ zawsze istnieje możliwość złamania poszczególnych procedur. Na przykład naukowcy odkryli niedawno pierwsze ataki na funkcję skrótu SHA-1. Opracowanie zupełnie nowego systemu tylko dlatego, że poszczególne komponenty uległy uszkodzeniu, jest po prostu zbyt kosztowne. Co więcej, niepewność dotycząca poszczególnych instancji nie zmienia faktu, że koncepcja jako taka jest bezpieczna. Aby zilustrować ten punkt, wystarczy pomyśleć ochronie przeciwpożarowej. To, że materiał, z którego wykonano pojedyncze drzwi, okazał się nie być ognioodporny, nie oznacza, że cała strategia, która przewidywała drzwi ognioodporne w określonym miejscu, jest błędna.
Krok 4: Formalny matematyczny dowód bezpieczeństwa
Po formalnym określeniu właściwości zabezpieczeń i projektu, w czwartym kroku następuje formalny matematyczny dowód bezpieczeństwa. Ten krok potwierdza, że projekt spełnia pożądane wymogi. Formalny dowód zapewnia mapowanie jeden-do-jednego między właściwościami zabezpieczeń bazowych bloków kryptograficznych a właściwościami zabezpieczeń, które system ma osiągnąć. Formalna weryfikacja zabezpieczeń ujawnia wady projektowe. Jeśli właściwości bezpieczeństwa bazowego budynku kryptograficznego nie zostaną zastosowane, oznacza to wadę projektu i najprawdopodobniej istnieje bardziej wydajne rozwiązanie.
Krok 5: Wykonaj implementację
Po ustanowieniu formalnego bezpieczeństwa systemu konieczne jest utworzenie instancji ogólnych kryptograficznych bloków konstrukcyjnych za pomocą określonych procedur kryptograficznych. Jeśli na przykład wprowadzono ogólny schemat szyfrowania z kluczem prywatnym, ten blok konstrukcyjny jest realizowany w praktyce przy użyciu AES. Ponieważ ogólne bloki konstrukcyjne działają z obiektami abstrakcyjnymi (takimi jak „klucz prywatny” lub „zaszyfrowany tekst”), musimy przetłumaczyć te obiekty na konkretne instancje. Na przykład obiekt „schemat szyfrowania wykorzystujący klucz publiczny” jest tworzony za pomocą schematu szyfrowania ElGamal [2].
Krok 6: Analiza bezpieczeństwa implementacji
Szósty i ostatni krok wymaga oceny bezpieczeństwa konkretnej instancji. Jest to wymagane, ponieważ podczas przejścia od abstrakcyjnego opisu do konkretnej implementacji czyha na nas wiele pułapek. Na przykład podstawowym elementem kryptograficznym używanym w połączniu z zabezpieczeniami protokołu internetowego (IPsec), znanym jako encrypt-then-MAC, jest uwierzytelniony schemat szyfrowania o słabym bezpieczeństwie [3]. Uważa się, że zabezpiecza on przed atakiem z dostępnym tekstem jawnym (CPA) [4], a także przed podszywaniem się, zważywszy, że schemat szyfrowania jest odporny na ataki CPA, a kod uwierzytelniania wiadomości (MAC) nie może zostać sfałszowany. Jednak konkretna instancja używana na przykład w protokole IPsec okazała się niepewna. O bezpieczeństwie wdrożenia mogą też świadczyć testy penetracyjne ujawniające słabości w implementacji koncepcji bezpieczeństwa, które mogłyby umożliwić atakującemu przeniknięcie do systemu.
Przykład: bezpieczna poczta elektroniczna
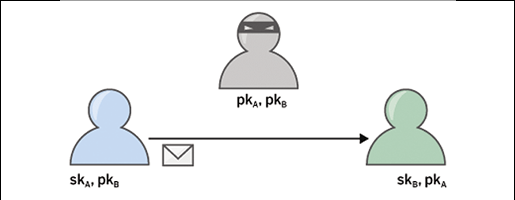
Aby zilustrować zasadę tworzenia oprogramowania w sposób dający się udowodnić, rozważmy przykład zaszyfrowanej wiadomości e-mailowej (Rysunek 2): Alicja chce wysłać zaszyfrowaną wiadomość do Boba, a Bob musi mieć możliwość odszyfrowania tej wiadomości i zweryfikowania użytego podpisu.
Alicja dysponuje kluczem publicznym Boba, pkB. Dla uproszczenia przyjmiemy, że Alicja zweryfikowała klucz i upewniła się, że faktycznie należy on do Boba. Ponadto Alicja ma swój własny klucz prywatny skA. Podobnie Bob zna klucz publiczny Alicji pkA i ma swój własny klucz prywatny skA. W tym przypadku założymy również, że Bob zweryfikował autentyczność klucza pkA.
Pierwszym krokiem jest określenie funkcjonalności. W tym przypadku mamy do czynienia z uwierzytelnioną pocztą elektroniczną; w związku z tym mamy dwa zadania: po pierwsze, musimy obliczyć zaszyfrowaną i uwierzytelnioną wiadomość e-mail. Ten interfejs jest oznaczony jako Enc+Auth. Po drugie, zakładając, że uwierzytelnianie jest prawidłowe – zaszyfrowana wiadomość musi zostać odszyfrowana. Trzymając się tego samego wzorca, oznaczymy ten interfejs jako Vrfy+Dec.
Drugim krokiem jest określenie (dość prostych) właściwości zabezpieczeń. Atakujący zna klucze publiczne Alicji i Boba oraz wszystkie zastosowane metody. Niemniej jednak osoba atakująca nie może uzyskać informacji zawartych w wiadomości. Ponadto atakujący nie może wysyłać wiadomości w imieniu Alicji (tj. wiadomości zweryfikowanych za pomocą klucza publicznego pkA) do Boba.
Chociaż te cechy wydają się mieć sens na poziomie intuicyjnym, nadal pozostawiają zbyt duże pole do interpretacji. Czy atakujący może wchodzić w interakcję z Bobem? Czy istnieje faza nauki, w której atakujący może używać Alicji jako interfejsu do przesyłania zaszyfrowanych i uwierzytelnionych wiadomości e-mail od Alicji do Boba? Czy atakujący może przez jakiś czas podszywać się pod Boba i czytać zaszyfrowane wiadomości e-mail? Jak generowane są wiadomości do Boba? W formalnym opisie właściwości bezpieczeństwa ważne jest wyeliminowanie tych niejednoznaczności, tak aby powstał dokładny i jednoznaczny opis.
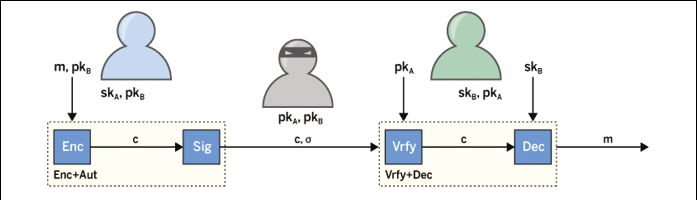
Po sformalizowaniu interfejsów i właściwości bezpieczeństwa trzecim krokiem jest utworzenie instancji poszczególnych komponentów przy użyciu metod kryptograficznych. Dwa interfejsy Enc+Auth i Vrfy+Dec muszą być skonstruowane za pomocą procedur kryptograficznych tak, aby zapewniały dokładnie pożądane funkcje. W przypadku bezpiecznej poczty ten krok jest stosunkowo prosty (Rysunek 3).
Aby zaimplementować interfejs Enc+Auth, musimy najpierw zaszyfrować wiadomość metodą klucza publicznego, a następnie podpisać szyfrogram metodą podpisu cyfrowego. Użyjemy c do oznaczenia zaszyfrowanego tekstu i małej greckiej litery sigma (s) do oznaczenia podpisu. Zgodnie z tym zaimplementowalibyśmy interfejs Vrfy+Dec z następującymi operacjami. Po pierwsze, algorytm weryfikacji procedury podpisu służy do sprawdzenia poprawności podpisu w zaszyfrowanym tekście c. Jeśli ta sygnatura jest prawidłowa, algorytm deszyfrujący procedury klucza publicznego odszyfrowuje tekst zaszyfrowany c i wyświetla wynikowy komunikat m.
W walidacji bezpieczeństwa w czwartym kroku możemy teraz założyć, że zarówno metoda szyfrowania, jak i metoda podpisu są bezpieczne i zgodne z formalnymi definicjami. Następnie formalnie weryfikujemy, czy atak łamiący zabezpieczenia Enc+Auth oraz Vrfy+Dec (zgodnie z modelem formalnym) może zostać użyty do złamania zabezpieczeń – zarówno klucza publicznego, jak i procedury podpisu. Ponieważ jednak obie procedury zostały w pierwszym kroku uznane za bezpieczne, powstaje sprzeczność, z której wynika, że taki atak nie może się powieść.
W ostatnich dwóch krokach stosujemy konkretne procedury, na przykład szyfrowanie oparte na RSA, wdrażamy je i potwierdzamy bezpieczeństwo wdrożenia za pomocą testów penetracyjnych.
Mocne strony i ograniczenia
Od czasu ich odkrycia metody kryptograficzne oparte na dowodach, takie jak szyfrowanie El Gamal [4], są praktycznie nie do złamania. Możliwe do udowodnienia bezpieczeństwo redukuje dowód na metodę szyfrowania do prostego problemu obliczeniowego, takiego jak bardzo dobrze znany problem faktoryzacji.
W tym zadaniu atakujący otrzymuje liczbę N=p × q obliczoną jako iloczyn dwóch liczb pierwszych o równej długości p oraz q. Zadaniem atakującego jest teraz obliczenie dwóch czynników pierwszych p i q. Do tej pory nie odkryto żadnego wydajnego algorytmu rozwiązania tego dobrze znanego problemu obliczeniowego. Jeśli bezpieczeństwo schematu szyfrowania jest teraz oparte na problemie faktoryzacji, to formalny dowód pokazuje, co następuje. Jeśli istnieje sprawny napastnik, który złamie schemat szyfrowania, to istnieje również sprawny napastnik, który rozwiąże problem faktoryzacji. Innymi słowy, problem złamania szyfrowania jest równie trudny do rozwiązania, jak problem faktoryzacji.
Na pierwszy rzut oka termin „udowodnione bezpieczeństwo” sugeruje, że dany system jest całkowicie odporny na ataki. To oczywiście nieprawda. Ataki na systemy, które uważa się za bezpieczne, zdarzają się bardzo często. Skąd bierze się ta sprzeczność i jak można ją rozwiązać? Przede wszystkim należy zauważyć, że bezpieczeństwo oparte na dowodzie zawsze odnosi się do modelu formalnego. Jeśli jednak model nie odzwierciedla w pełni praktyki, nie może wykluczyć potencjalnych ataków, ponieważ te ataki po prostu nie występują w modelu. W konsekwencji dokładne modelowanie rzeczywistości jest jednym z największych wyzwań w tym obszarze, a nawet najmniejsze błędy w modelowaniu mogą prowadzić do niepewnego rozwiązania.
Doskonałym przykładem niepełnego modelowania jest bezpieczeństwo protokołu Secure Sockets Layer (SSL). W praktyce zdarzało się, że wiadomość nie została odszyfrowana; zamiast tego pojawiał się komunikat Padding Error. Na pierwszy rzut oka wydaje się to nieszkodliwe, ponieważ nie wydaje się ujawniać żadnych bezpośrednich informacji na temat tekstu jawnego, zatem nie uwzględniono tego w formalnym modelu. Później jednak badaczom udało się wykazać, że możliwe jest wykorzystanie tego komunikatu o błędzie do odszyfrowania całej wiadomości – i to bez naruszania rzeczywistego bezpieczeństwa schematu szyfrowania.
Typowe błędy
Każda osoba zajmująca się bezpieczeństwem powie nam, że nigdy nie należy opracowywać własnej metody kryptograficznej; wiele osób powtarza tę opinię jak mantrę. Jednak kiedy zagłębimy się w temat, może się okazać, że ustalenie momentu, od którego zaczyna się tworzenie własnej procedury, nie jest wcale proste. W istocie mantra ta jest nieprecyzyjna i powinna brzmieć: „Nigdy nie używaj procedur kryptograficznych, chyba że potrafisz udowodnić, co robisz”. Poniższy przykład pokazuje, że to stwierdzenie nie jest w żaden sposób przesadzone i że nawet proste użycie dwóch procedur kryptograficznych może prowadzić do całkowicie niepewnej konstrukcji.
W tym przykładzie załóżmy, że Alicja chce przechowywać plik m z szyfrowaniem w chmurze. W tym celu wykorzystuje wiadomość i klucz publiczny. Operator chmury nie chce przechowywać duplikatów tej samej wiadomości ze względu na wydajność. Jednak ponieważ plik został zaszyfrowany, operator nie może łatwo określić, czy wiadomość już istnieje w postaci zaszyfrowanej w chmurze.
Z tego powodu tekst zaszyfrowany jest rozszerzony o wartość skrótu wiadomości: c = (Enc(pk,m), H(m)). Funkcja mieszająca to funkcja deterministyczna, która zwykle kompresuje dane wejściowe. Bezpieczeństwo tej funkcji opiera się na odporności na kolizje. Ta właściwość oznacza, że (w praktyce) niemożliwe jest znalezienie dwóch różnych komunikatów m1 i m2, które dają ten sam wynik (H(m1) = H(m2)).
Intuicyjnie można się spodziewać, że – dzięki właściwościom kompresji – wartość skrótu nie ujawnia żadnych informacji o wiadomości m. Jednak nie istnieje właściwość zabezpieczająca, która obejmuje to założenie. W rzeczywistości analiza konstrukcji pokazuje, że jest ona całkowicie niepewna. W szczególności dane wyjściowe funkcji mieszającej można wykorzystać do całkowitego zastąpienia właściwości bezpieczeństwa szyfrowania.
Ten prosty przykład ilustruje, że połączenie dwóch bezpiecznych metod kryptograficznych może prowadzić do niezabezpieczonej konstrukcji. Metody kryptograficzne powinny być używane razem tylko wtedy, gdy rzeczywiście potrzebujemy właściwości bezpieczeństwa każdej metody. Formalnie udowadnia się właśnie ten związek między podstawowymi właściwościami a właściwościami, na których nam zależy.
Aktualne tematy badawcze
W dziedzinie badań nad kryptografią wciąż istnieją niezliczone nierozwiązane problemy. Tematycznie badacze poruszają się między podstawowymi badaniami teoretycznymi a stosowanymi badaniami praktycznymi. W tej części przedstawimy dwa obszary aktualnych badań.
Jednym z nich jest kryptografia oparta na hasłach. Hasła są piętą achillesową wielu nowoczesnych systemów, ponieważ łączą w sobie wszystko, co dla kryptografa jest niepożądane: są krótkie i mają niewielką entropię, co oznacza, że atakujący może złamać większość haseł, po prostu je wypróbowując. Ten rodzaj ataku jest znany jako atak siłowy w trybie offline. Po wynalezieniu kryptografii klucza publicznego wielu spekulowało, że hasła wyginą i wszyscy będą używać do uwierzytelniania wyłącznie klucza prywatnego. Do tej pory tak się nie stało i wydaje się, że hasła pozostaną najpopularniejszą techniką uwierzytelniania w Internecie na dłuższą metę. Badacze zastanawiają się więc, w jaki sposób można zagwarantować bezpieczeństwo systemu, nawet jeśli używa on słabych sekretów, takich jak hasła.
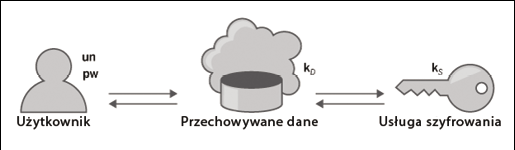
W tym kontekście opracowano wzmacnianie hasła i szyfrowanie go (PHE) (Rysunek 4). Pomysł opiera się głównie na następujących rozważaniach. Po pierwsze, interfejs użytkownika nie może się zmienić, więc nadal używa on swojej nazwy użytkownika i hasła do uwierzytelniania. Po drugie, dane użytkownika muszą być odporne na ataki siłowe w trybie offline – nawet jeśli baza danych została skradziona. I po trzecie, aby to osiągnąć, potrzebujemy zewnętrznej usługi kryptograficznej, która nie ma bezpośredniego dostępu do danych, a jedynie zapewnia operacje szyfrowania i odszyfrowywania danych.
Szyfrowanie wzmocnione hasłem zapewnia poziom bezpieczeństwa, który był wcześniej nie do pomyślenia. Po raz pierwszy dane użytkownika mogą być przechowywane w sposób zabezpieczony przed atakami siłowymi przeprowadzanymi w trybie offline, bez konieczności używania przez użytkownika skomplikowanych technik klucza publicznego.
Drugi obszar badań dotyczy obliczeń wykonywanych na zaszyfrowanych danych. Aby lepiej zrozumieć, w jaki sposób można wykonywać obliczenia na zaszyfrowanych danych, zastanówmy się, jak działa konwencjonalne szyfrowanie.
Niezależnie od rodzaju metody szyfrowania, każda metoda zasadniczo zapewnia generowanie, szyfrowanie i odszyfrowywanie kluczy. Ponieważ generowanie kluczy nie odgrywa roli w poniższych rozważaniach, nie będziemy wchodzić w szczegóły tej operacji.
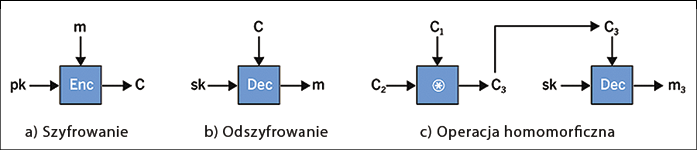
W kryptografii operacja szyfrowania to procedura, która konwertuje czytelny tekst, czyli tekst jawny, do postaci, która nie ujawnia już żadnych informacji o tekście jawnym – czyli tekst zaszyfrowany. Rysunek 5 obrazuje operację szyfrowania i deszyfrowania. Algorytm szyfrowania Enc pobiera komunikat m oraz klucz publiczny pk jako dane wejściowe. Wynikiem obliczeń jest tekst zaszyfrowany c. Do odszyfrowania używany jest algorytm deszyfrowania Dec, który jako dane wejściowe przyjmuje tajny klucz sk i zaszyfrowany tekst c.
Aby opisać homomorficzną metodę szyfrowania, musimy najpierw wprowadzić pojęcie homomorfizmu. Pochodzi ono z matematyki i oznacza mapowanie z zachowaniem struktury. Mówiąc prościej, oznacza to, że możemy odwzorować wykonanie obliczeń w danej strukturze na obliczenia w innej strukturze, przy czym sama struktura zostaje zachowana.
Koncepcja homomorfizmu jest obecnie stosowana do metod szyfrowania. Oznacza to wykonanie obliczeń na zaszyfrowanym tekście bez faktycznego odszyfrowywania zaszyfrowanego tekstu. Cechą szczególną tej operacji jest to, że obliczenia na tekście jawnym mają wpływ na tekst zaszyfrowany, chociaż tekst jawny nie jest dostępny podczas tych obliczeń. W zależności od rodzaju szyfrowania kombinacja zaszyfrowanych tekstów jest stosowana do tekstu jawnego jako dodawanie lub mnożenie. Operacja dodawania jest znana jako addytywne szyfrowanie homomorficzne, a operacja mnożenia nazywana jest multiplikatywnym szyfrowaniem homomorficznym.
Proces ten widzimy na prawej połowie Rysunku 5. Po lewej stronie widać dwa szyfrogramy: C1 i C2. Zostały one obliczone w sposób konwencjonalny, czyli C1 jest wynikiem zaszyfrowania wiadomości m1 kluczem publicznym pk, natomiast C2 jest wynikiem zaszyfrowania wiadomości m2 kluczem publicznym pk. Te dwa szyfrogramy są teraz łączone przez obliczenie x.
Tytułem przykładu najpierw zaszyfrujemy cyfrę 2 kluczem publicznym pk: C1 := Enc(pk,2). Wynikowy tekst zaszyfrowany jest określany jako C1. W drugim kroku wykonujemy te same kroki z liczbą 3: C2 := Enc(pk,3), by wygenerować zaszyfrowany tekst C2. Trzeci krok łączy oba szyfrogramy, wykonując operację x: C3 := C1 x C2. Jeśli metoda szyfrowania jest addytywną metodą homomorficzną, to zaszyfrowany tekst C3 := C1 x C2 := Enc(pk,2) x Enc(pk,3) = Enc(pk,2+3) = Enc(pk ,5) zawiera wartość 5. Jeśli proces jest multiplikatywnie homomorficzny, to C3 := C1 x C2 := Enc(pk,2) x Enc(pk,3) = Enc(pk,2 *3) = Enc(pk,6), czyli zawiera wartość 6.
W obu przypadkach tylko właściciel tajnego klucza sk ma dostęp do wyniku obliczeń, ponieważ tylko on może odszyfrować zaszyfrowany tekst C3. Przykładu addytywnego szyfrowania homomorficznego dostarcza metoda ElGamala [2], natomiast metoda Pailliera [5] jest homomorficzna multiplikatywnie.
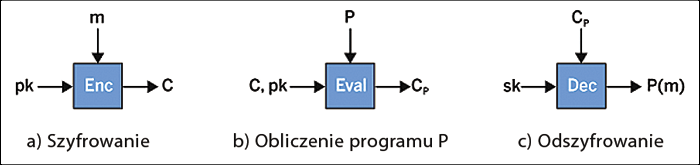
W przeciwieństwie do poprzednich metod, szyfrowanie w pełni homomorficzne umożliwia wykonywanie dowolnych obliczeń na zaszyfrowanym tekście. Aby lepiej zrozumieć, jak to działa, przyjrzyjmy się poszczególnym krokom przedstawionym na Rysunku 6. Po pierwsze, zwykły tekst m jest zaszyfrowany kluczem publicznym pk(a), w wyniku czego powstaje zaszyfrowany tekst C. Następnie wykonywane jest obliczenie (b), które wykorzystuje zaszyfrowany tekst C, klucz publiczny pk oraz opis programu P. Wynikiem obliczeń jest tekst zaszyfrowany CP, a wynik obliczenia to Eval(pk,C,P) = CP = Enc(pk,P(m)).
Podobnie jak w poprzednich przykładach, każdy może wykonać obliczenia na zaszyfrowanym tekście C, ponieważ nie wymaga on żadnych tajnych informacji. Jednak tylko właściciel skojarzonego klucza tajnego sk może obliczyć wynik. Szyfrowanie w pełni homomorficzne jest niezwykle potężnym narzędziem, ponieważ nie ma ograniczeń dla programu P. Oznacza to, że na zaszyfrowanych danych można wykonywać dowolne obliczenia. Wykonywanie obliczeń na zaszyfrowanych danych znacznie zmniejsza potrzebę zaufania do podmiotu przechowującego dane. Możemy na przykład przekazać dane firmie oferującej usługi chmurowe – może ona przechowywać dane i wykonywać na nich obliczenia bez konieczności odszyfrowywania ich. Usługa wykonująca obliczenia nie musiałaby widzieć danych w postaci zwykłego tekstu ani nawet wyniku obliczeń – właściciel danych zachowuje nad nimi pełną kontrolę.
Wnioski
W niniejszym artykule przedstawiliśmy podstawy bezpieczeństwa opartego na dowodach, które jest jednym z fundamentów współczesnej kryptografii. Wspomnieliśmy też o najnowszych trendach, które budzą ekscytację kryptologów.
Kryptografia istnieje od tysięcy lat, a mimo to nadal jest interesująca – najnowocześniejsze techniki szyfrowania mogą sprawiać wrażenie magicznych. Na przykład, kto by pomyślał, że obliczenia na zaszyfrowanych (genetycznych) danych będą działać? Co więcej, patrząc na całościową historię rozwoju nauki, można być pewnym, że kryptografia jest wciąż w powijakach, a przyszłe technologie kryptograficzne bez wątpienia będą nas nadal zaskakiwać.




